Jika sebelumnya kita telah membahas apa itu fisika dan juga besaran apa saja yang ada di fisika maka di posting kali ini kita akan membahas Besaran Skalar dan Vektor. Simak baik-baik postingan ini jika kalian benar-benar ingin memahami fisika. selamat belajar!
1. Besaran Skalar dan Vektor
Besaran-besaran fisika secara umum dapat dikelompokkan menjadi tiga jenis, besaran skalar, besaran vektor
dan besaran tensor. Untuk besaran tensor, tidak akan dipelajari dalam pelajaran fisika dasar. Besaran skalar
adalah besaran yang memiliki nilai saja, sedangkan besaran vektor adalah besaran yang selain memiliki nilai
juga memiliki arah. Karena konsep tentang vektor banyak digunakan dalam fisika, maka akan dijelaskan
lebih lanjut secara singkat mengenai besaran vektor ini.
1.1 Vektor
Sebagai contoh untuk vektor, sekaligus sebagai dasar dari konsep vektor, adalah vektor posisi. Untuk
menentukan posisi sebuah titik relatif terhadap titik yang lain, kita harus memiliki sistem koordinat. Dalam
ruang berdimensi tiga, dibutuhkan sistem koordinat x, y, z untuk mendiskripsikan posisi suatu titik relatif
terhadap suatu titik asal (O). Sistem koordinat x, y, z ini sering disebut sebagai sistem koordinat kartesan.
Dalam penentuan arah positif setiap sumbu, dipakai kesepakatan putar kanan (tangan kanan). Yaitu dari
bila diputar dari arah positif x ke arah positif y, putarannya mengarah ke arah positif z.
Vektor posisi suatu titik P, relatif terhadap titik asal pada bidang digambarkan di bawah ini.
1.2. Penjumlahan Vektor
Dari konsep vektor posisi dikembangkan konsep penjumlahan vektor. Misalkan vektor posisi titik A adalah
A~, sedangkan posisi titik B ditinjau dari titik A adalah B~ . Vektor posisi titik B adalah vektor C~ , dan C~
dapat dinyatakan sebagai jumlahan vektor A~ dan vektor B~ , A~ + B~ = C~ .
Negatif dari suatu vektor A~ dituliskan sebagai −A~ dan didefinisikan sebagai sebuah vektor dengan besar
yang sama dengan besar vektor A~ tetapi dengan arah yang berlawanan, sehingga A~ + (−1)A~ = 0. Dari sini konsep pengurangan vektor muncul, jadi
Aljabar vektor bersifat komutatif dan asosiatif. Jadi
Dalam ruang berdimensi tiga terdapat paling banyak tiga vektor yang dapat saling tegak lurus. Vektorvektor
yang saling tegak lurus ini dapat dijadikan vektor-vektor basis. Dalam sistem koordinat kartesan,
sebagai vektor-vektor basis biasanya diambil vektor-vektor yang mengarah ke arah sumbu x, y, dan z positif,
dan diberi simbol ˆx, ˆy, dan ˆz. Vektor-vektor basis ini juga dipilih memiliki besar satu satuan. Sehingga
sembarang vektor A~ dalam ruang dimensi tiga dapat dinyatakan sebagai jumlahan vektor-vektor basis dengan
koefisien-koefisien Ax, Ay, Az yang disebut sebagai komponen vektor dalam arah basis x, y dan z.
Dari trigonometri dapat diketahui bahwa bila sudut antara vektor A~ dengan sumbu x, y, dan z adalah
θx, θy, dan θz, maka Ax = A cos θx, Ay = A cos θy, dan Az = A cos θz, dengan A adalah besar A~. Dari
teorema Phytagoras, diperoleh bahwa
1.3 Perkalian Vektor
Dua buah vektor dapat ‘diperkalikan’. Konsep perkalian antar vektor sangat bermanfaat dalam perumusan
berbagai persamaan-persamaan fisika. Konsep perkalian dalam vektor sangat berbeda dengan sekedar
memperkalian dua buah bilangan (skalar), dan memiliki definisi tersendiri. Dua buah vektor dapat diperkalikan
menghasilkan sebuah skalar ataupun sebuah vektor baru. Perkalian yang menghasilkan skalar disebut
sebagai perkalian skalar atau perkalian titik (dot product), dan didefinisikan sebagai
dengan θ adalah sudut antara vektor A~ dan B~ . Besar vektor C~ = A~+B~ dapat dinyatakan dalam perumusan
berikut ini
Bila A~ dan B~ dinyatakan dalam komponen-komponennya,
maka
Persamaan di atas diperoleh setelah melakukan perkalian skalar basis-basis vektornya, yaitu
Dengan mengalikan sembarang vektor A~ dengan sebuah vektor basis, akan didapatkan proyeksi A~ ke arah vektor basis tadi, jadi
misalnya A~ · xˆ = Ax. Alternatif definisi perkalian skalar dapat dimulai dari pers. (1.2), kemudian pers. (1.1)
dijabarkan darinya.
Perkalian dua buah vektor yang menghasilkan sebuah vektor, disebut sebagai perkalian silang (cross
product), untuk dua buah vektor A~ dan B~ dituliskan
Vektor C~ di sini adalah suatu vektor yang arahnya tegak lurus terhadap bidang di mana A~ dan B~ berada,
dan ditentukan oleh arah putar tangan kanan yang diputar dari A~ ke B~ . Besar vektor C~ didefinisikan sebagai
Sekian untuk pembahasan fisika kita kali ini.








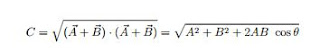








0 comments:
Post a Comment